Motion Planning For Autonomous Vehicles Based On Sequential Optimization
A novel mathematical approach for planning the autonomous vehicle motion in a constrained space
This article is a part of our University Technology Exposure Program. The program aims to recognize and reward innovation from engineering students and researchers across the globe.
Introduction
The article presents a concise description of the mathematical approach for planning the autonomous vehicle (AV) motion in a constrained space.
From the point of view of reducing the necessary procedures in motion planning, simultaneous optimization of the trajectory and kinematic parameters would be preferable. However, with such an approach, it is difficult to satisfy all criteria, which often contradict each other, and the final objective function requires detailed study. In contrast, the proposed technique offers a two-stage prediction of the AV motion, demonstrating its mathematical logicality, clarity, workability, and efficiency on a generalized example of curvilinear movement in conditions of external boundaries and a moving obstacle.
What is the technology about? An overview
The submission represents an overview of the developed technique for planning the AV motion reference parameters. The predictions of trajectory, speed, acceleration, and other AV's kinematic parameters are determined using sequential optimization. The proposed approach combines the basic principles of the finite element method (FEM) and nonlinear optimization with nonlinear constraints.
First, the generalization on representing an arbitrary function by finite elements (FE) is briefly described. A one-dimension FE with two nodes and three degrees of freedom (DOF) in a node was chosen as the basic one, corresponding to the 5th-degree polynomial.
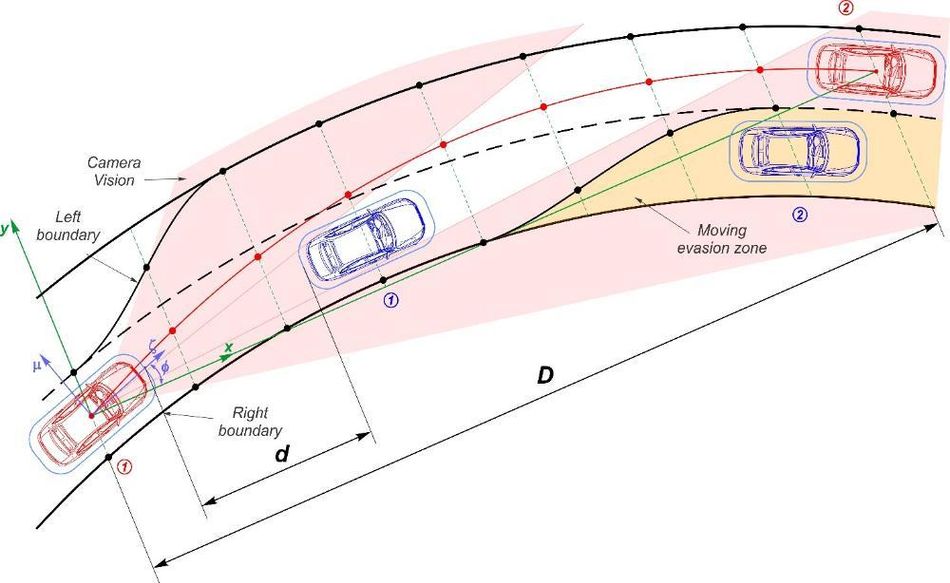
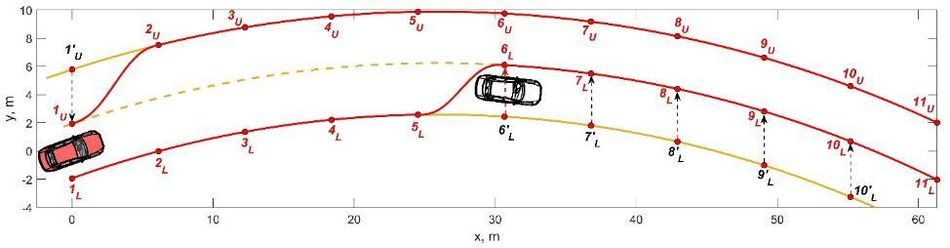
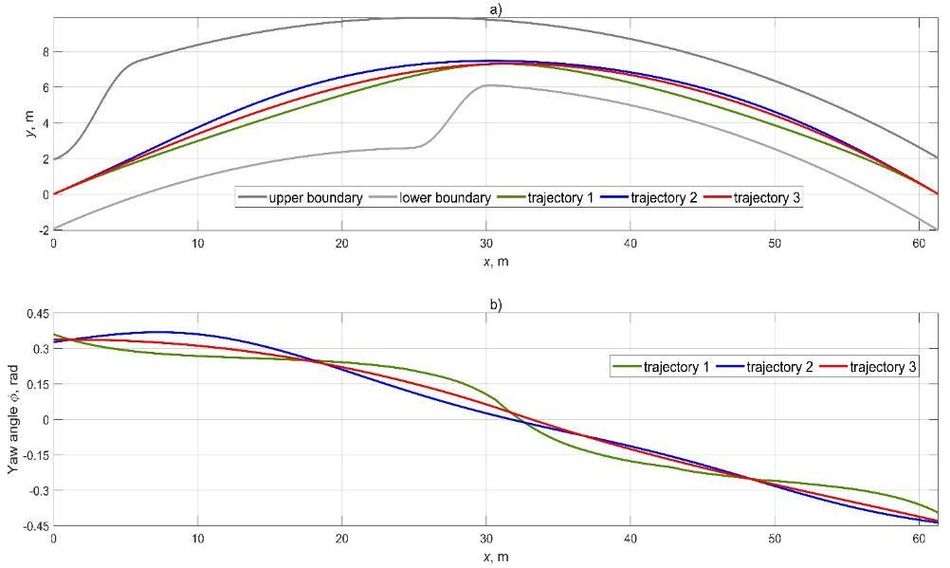
Next, a method for determining the motion trajectory is developed. The following are considered: formation of a restricted space for the AV's allowable maneuvering, the geometry of motion trajectory and its relation with vehicle steerability parameters, cost functions and their influences on the desirable trajectory's nature, compliance of nonlinear restrictions of the node parameters with the motion area boundaries. At the second stage, a technique for optimizing AV speed and acceleration redistribution is elaborated.
The model considers possible combinations of cost functions, conditions of limiting the kinematic parameters with the tire slip critical speed, maximum speed level, maximum longitudinal acceleration, and critical lateral acceleration. In the simulation section, several variants of trajectories were searched and compared. Several versions of distributing the longitudinal speed and acceleration curves are determined, and their comparative analysis is fulfilled.
What sub-systems is technology composed of?
The mechanism of forming the boundaries of permissible movement in the presence of a movable obstacle is stipulated. Criteria for finding optimal trajectory plans and distribution of kinematic parameters are determined and analyzed, considering geometric, kinematic, and physical restrictions, including the vehicle performance potential. A series of virtual tests have been carried out for the generalized example of searching for motion predictions, demonstrating the consistency of the proposed technique and the quality of the resulting plans.
What tasks do they fulfill?
The first stage is based on ensuring movement safety in the zone of admissible boundaries and stability of control due to the optimal smoothness of the predicted trajectory, considering the geometric and kinematic characteristics of the AV model. The second stage ensures the distribution of kinematic parameters along the trajectory length, the main of which are the longitudinal speed and acceleration, based on minimizing the complex criteria determined by the internal vehicle potential and the physics of tire-road interaction. The geometric, kinematic, and physical nonlinear constraints used in the optimization steps contribute to the realism and feasibility of the proposed planning technique.
How are these sub-systems integrated?
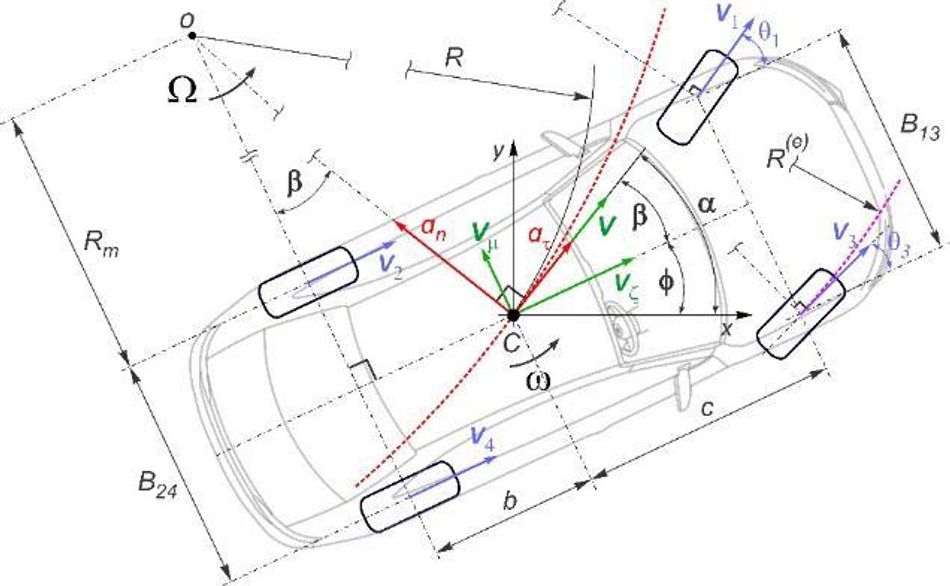
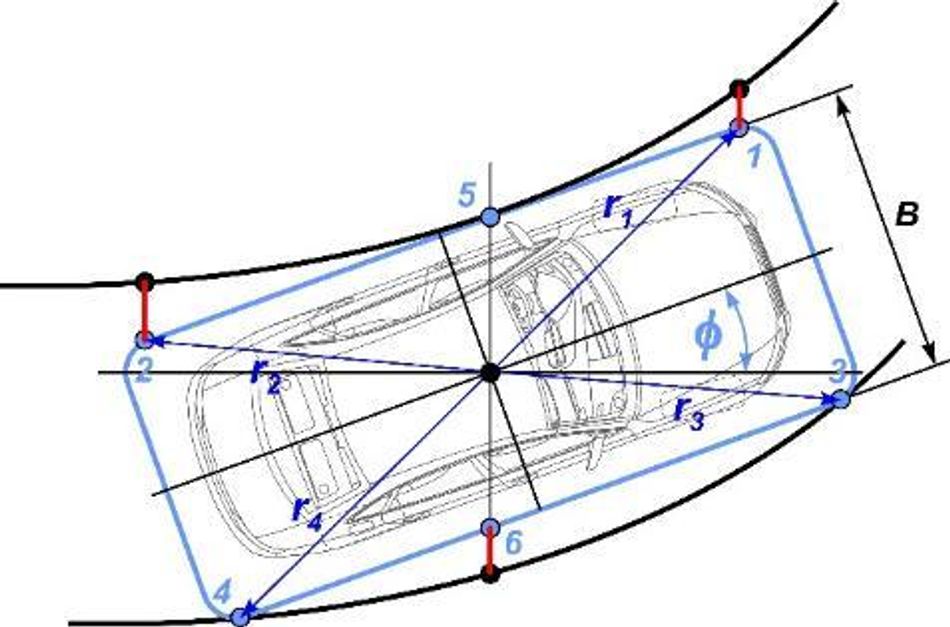
To test the approach proposed, several variants of planning trajectories and speeds were performed based on the composed MATLAB code using the basic nonlinear optimization function fmincon. The primary necessary physical, kinematic, and geometric data (Fig. 3) of the vehicle Audi A4 Quattro were used.
Were any issues/obstacles resolved through clever component reengineering or innovative solutions?
From the point of view of reducing the necessary procedures in motion planning, simultaneous optimization of the trajectory and kinematic parameters would be preferable. However, with such an approach, it is difficult to satisfy all criteria, which often contradict each other, and the final objective function requires detailed study. In contrast, the proposed technique offers a two-stage prediction of the AV motion, demonstrating its mathematical logicality, clarity, workability, and efficiency on a generalized example of curvilinear movement in conditions of external boundaries and a moving obstacle.
Supporting materials (technical drawings, schematics, illustrations, animations, etc.)
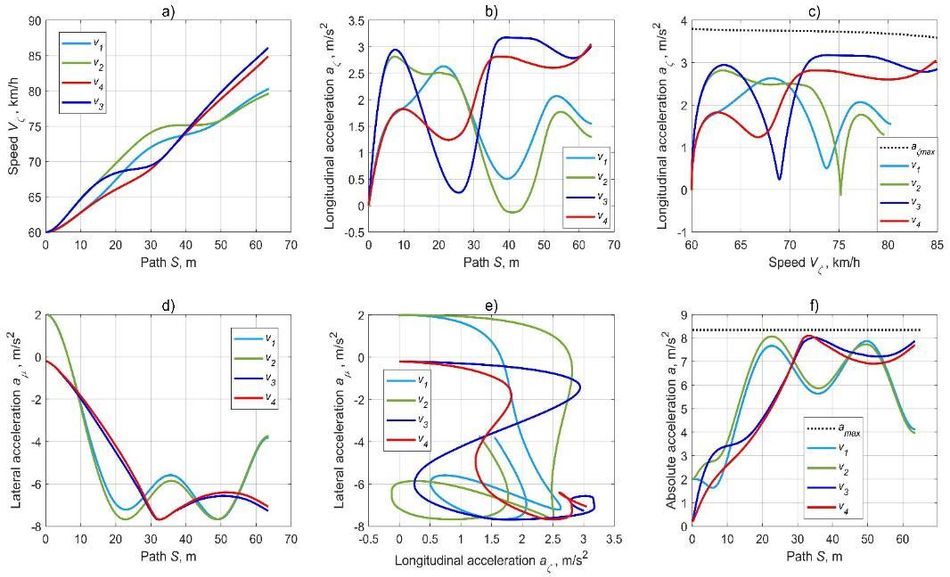
a) longitudinal speed along the trajectory,
b) longitudinal acceleration along the trajectory
c) longitudinal acceleration along with the longitudinal speed
d) lateral acceleration along the trajectory
e) relation between longitudinal and lateral accelerations
f) absolute acceleration along the trajectory
What are the different applications of the technology?
Planning the AV motion is characterized by using various techniques and many of which originate from the tasks of modeling trajectories for robots. The difference from planning for robots lies primarily in the fact that vehicles are high-speed unsafe transport means and the significant influence of physical characteristics of the vehicle-road interaction. Another planning option is the search for continuous functions defined in the space domain based on the optimization process in the presence of geometric, kinematic, and physical characteristics restrictions limiting the vehicle-road interaction. The root-mean-square curvature of an optimized path within the trajectory boundaries can be much less than one of a trajectory built by midpoints.
The optimization settings can be tuned concerning the type of vehicle drivetrain and the presence of intelligent traction control systems. As shown in Fig. 6b, entering the second lane's corridor is possible with acceleration and deceleration. The first technique is more typical for vehicles with front-wheel drive, while the second fits rear-wheel drive. With Torque Vectoring or Sport Differential technology, the nature of the control plans can be more intense towards higher speeds and accelerations.
For planning the AV kinematic parameters, it is recommended to focus on the criteria that ensure using a speed close to the desired level in a quadratic sense and a compromise between the intensities of longitudinal speeds and accelerations. The latter provides both smoothness of speed and acceleration (Fig. 6a, 6b). At the same time, it is desirable to choose the weighting coefficients' balance in such a way to preserve the physical capability of reproducing such control laws on an actual vehicle. This might occur when the transient delay problem arises due to the features of the vehicle propulsion system. If the acceleration prediction requires only non-negative values, the minimum acceleration value in the constraints must be set to a negative value close to 0. First, this will narrow the range of scattering and search for accelerations. Second, it will exclude the variants with more significant negative acceleration values, which would mean the need for using the braking system. Thus, the weighting coefficients must correspond to the task of maintaining a speed mode.
How does it affect the industry and/or society?
A distinctive feature of the proposed technique is an explicit restriction of the safe motion area with optimizing the best trajectory choice in contrast to the approaches focused on conjugating the lanes' midpoints by smooth curves. The fundamental advantage of the proposed approach consists of obtaining a significant number of reference curves (Fig. 6) mathematically related to each other, which contributes to improving the quality of AV control in tracking. The forecasting stability is ensured by the smoothness of the higher derivative functions of the desired trajectory and speed distributions. Furthermore, the vehicle has a sensory system (MEMS gyroscopes and accelerometers, wheels' angular speed sensors) capable of evaluating in real-time the longitudinal speed, longitudinal and lateral accelerations, yaw rate, and other parameters directly. Thus, in organizing the tracking of AV references, the control accuracy is higher than only by controlling speed and lateral position.
About the University Technology Exposure Program 2022
Wevolver, in partnership with Mouser Electronics and Ansys, is excited to announce the launch of the University Technology Exposure Program 2022. The program aims to recognize and reward innovation from engineering students and researchers across the globe. Learn more about the program here.

References
[1] Diachuk, M.; Easa, S.M. Motion Planning for Autonomous Vehicles Based on Sequential Optimization. Preprints 2022, 2022020165 (doi: 10.20944/preprints202202.0165.v1).