Topology Optimization for a Bicycle Wheel
This is the first of a series of blogs (and presentations) focusing on Design for Additive Manufacturing in the context of Industrial Design. This blog explores topology optimization for a bike wheel focusing on three mutually perpendicular loads: radial loads, tangential loads, and lateral loads.
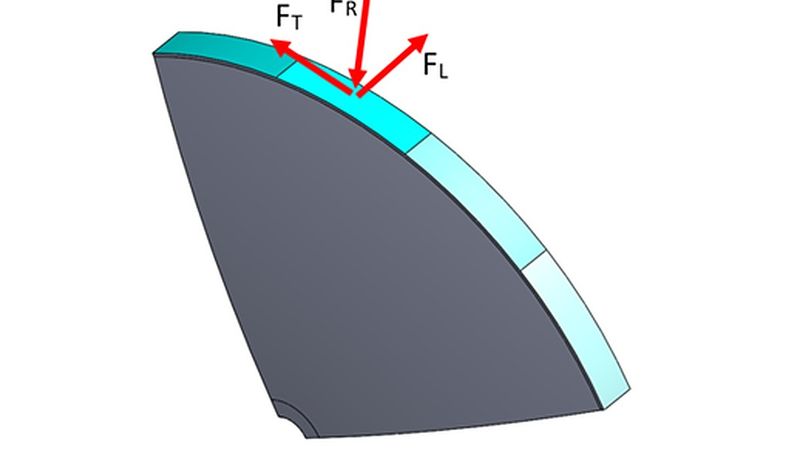
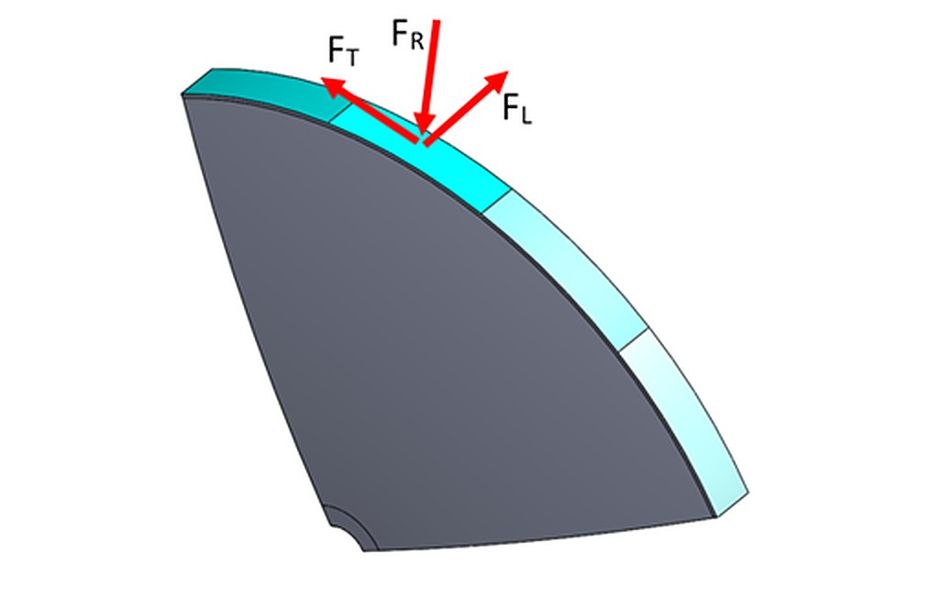
Fig.1: Derivation of Forces applied to the contact patch
This article was first published on
ntopology.comIntroduction
The modern bicycle wheel is a uniquely efficient structure comprised of tension-compression members to maximize structural rigidity. The modern concept of the bicycle wheel has its roots in the traditional compression wheel, the design of which still has its place in many applications today including most modern cars and a wide variety of motorcycles.
The optimization of compression wheels can significantly increase performance as a result of low rotational inertia while adequately distributing stress subject to a variety of distinct load cases. A bicycle was taken as just one embodiment of how this can be achieved through topology optimization.
In this study, the geometry of a compression style bicycle wheel was optimized using nTopology’s topology optimization algorithms to generate forms which efficiently distribute stress. Geometry was optimized for maximum stiffness at a set volume ratio subject to multiple distinct load cases. Data from literature is used to form a set of distinct load cases which were used to drive the topology optimization process. The resulting geometry was then assessed against the original load cases through finite element analysis to ascertain its efficacy and a scale model was created.
Setting up the model
A well-designed wheel should be able to adequately resist three mutually perpendicular loads: radial loads, tangential loads, and lateral loads. Two distinct complex load cases were considered:
- Hard braking, consisting of Radial loads (FR) and Tangential loads (FT)
- Lateral skid, consisting of Radial loads (FR) and Lateral loads (FL)
The design region considered for this study was based on a right angled section of a tapered disk. This model is further subdivided into another four sections to simulate a rolling contact patch across the wheel rim. Symmetry is enforced across the vertical plane and mid planes of the wheel section. The topology optimization is programmed to minimize the volume fraction while maximizing the model stiffness for each load case. The forces were modelled as acting uniformly over the contact patch as shown in the figure below.
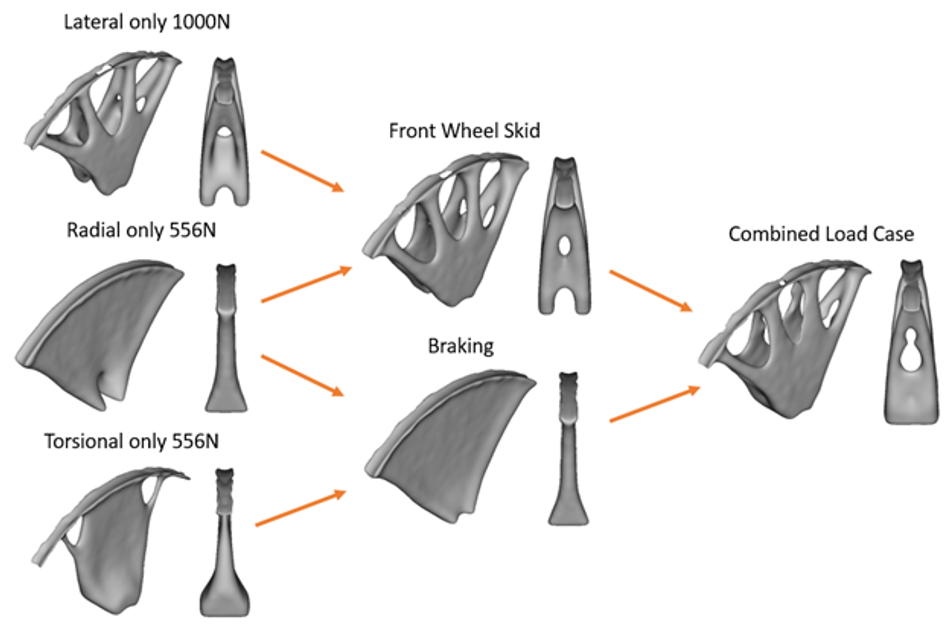
The optimum wheel geometry differed depending on the applied load cases. As a result, the ideal wheel geometry is highly dependent on the relative magnitude of the various load cases considered, making it very difficult to find a solution through traditional analytical means.
Using nTop Platform, outcomes could be easily investigated by simply varying the input parameters and iteratively running the same nTop workflow. The image below illustrates the evolution of optimum geometries by considering combinations of distinct load cases.
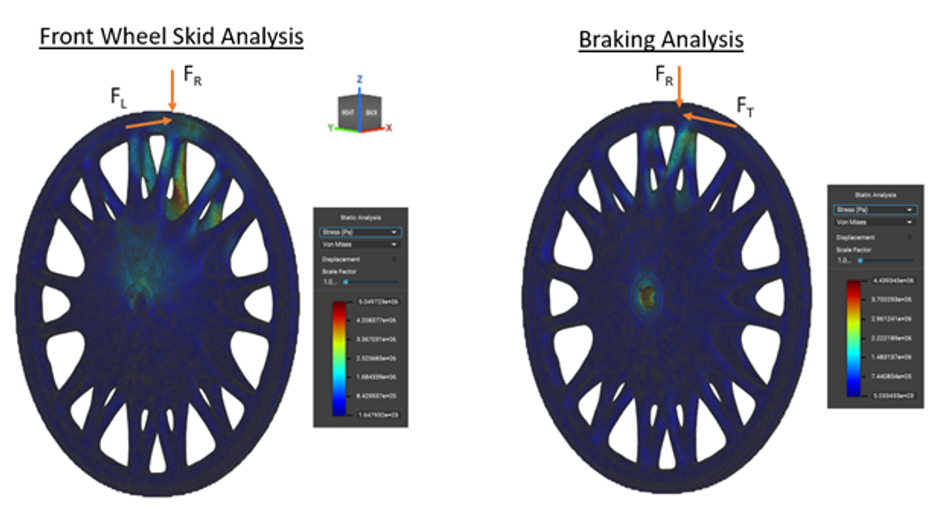
After the optimized geometry was patterned into a full wheel model, the resulting geometry was analyzed using finite element analysis to determine its effectiveness of stress distribution subject to complex combinations of load cases and was programmed within the same nTop Workflow.
It was found that the relative magnitudes of maximum stress subject to complex load cases typically found during the scenarios of front wheel skid and hard braking were within 0.6MPa. This finding illustrates that the resulting geometry is equally efficient at distributing stress when subjected to the unique set of load cases associated with lateral skids and hard braking.
Conclusion
nTop Platform proved to be an effective and adaptive tool for the creation of efficient geometries when catering for multiple (sometimes complex) load cases. The bicycle wheel was an excellent example of this, where distinct load cases generate different optimized geometries and the most efficient geometry for the combined load case cannot easily be deduced through analytical means. The basic analysis discussed in this article can easily be adapted to find optimal geometries for wheels of varying sizes as well as different load cases.
This article was first published on the nTopology blog.